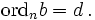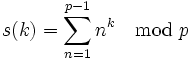POTD 2007-02
| Table of contents |
February 2007
Monday, 26th of February
from dedekind
for 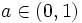 and
and 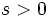 find:
find:
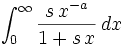
in terms of a famous "higher" function
Saturday, 24th of February
from Polytope
Define two sequences 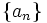 and
and 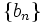 by
by
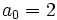 ,
, 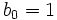 ,
,
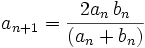 , and
, and 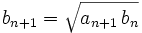 .
.
Show that 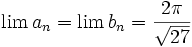
Here is a small hint.
Thursday, 22nd of February
from Crito
Find all positive integer pairs (a,n) such that 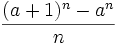 is an integer.
is an integer.
Solution by int-e
Wednesday, 21st of February
from Crito
Show that there exist infinitely many square-free positive integers n that divide 2005n − 1.
Solution by int-e
Tuesday, 20th of February
from Crito
Let  be positive real numbers such that
be positive real numbers such that 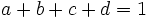 . Prove that
. Prove that
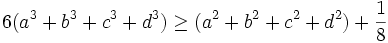
Solution from landen
Tuesday, 13th of February
from math channel discussion
For k a positive integer and p a prime, what are the possible values of:
Solutions from int-e (first solver) and landen (different method).
Saturday, 10th of February
Mathica
Suppose that 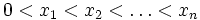 ; define the function f(t) on [0,xn] as the proportion of those xi that are
; define the function f(t) on [0,xn] as the proportion of those xi that are 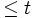 . Let g on [0,xn] be the least concave majorant of f, meaning the unique concave function everywhere
. Let g on [0,xn] be the least concave majorant of f, meaning the unique concave function everywhere 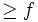 that is pointwise
that is pointwise 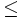 any other concave function that is pointwise
any other concave function that is pointwise 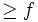 . Evaluate
. Evaluate 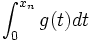 as a function of
as a function of 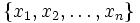 .
.
Tuesday, 6th of February
Crito
 is a natural number.
is a natural number. 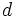 is the least natural number that for each
is the least natural number that for each 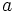 with
with 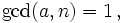 we have that
we have that 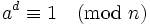 . Prove that there exists a natural number
. Prove that there exists a natural number 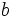 with
with