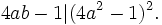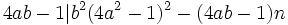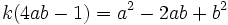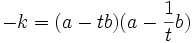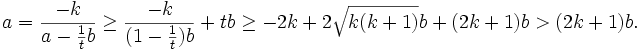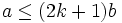Solution September 11, 2007
Solution
Assume for the sake of contradiction that we have a and b such that 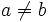 and
and
Then
With 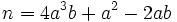 this gives
this gives
Let
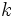 can not be
can not be 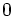 so we have
so we have  .
Choose
.
Choose 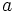 and
and 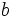 among the solutions of (1) such that
among the solutions of (1) such that 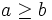 and
and 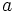 is minimal.
is minimal.
Then, on the one hand,
where 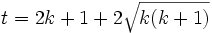 . Since
. Since 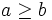 , the second term is positive, and
, the second term is positive, and
On the other hand, if 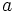 is a solution of (1) then so is
is a solution of (1) then so is 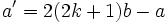 . By the minimality condition, we have
. By the minimality condition, we have 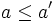 , i.e.
, i.e.
This is a contradiction to the previous inequality, completing the proof.