Solution June 03, 2007
Problem
i) Find all infinite arithmetic progressions of positive integers 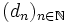 such that dp is prime for all sufficiently large primes p.
such that dp is prime for all sufficiently large primes p.
ii) Find all polynomials ![f(X) \in \mathbb{Z}[X]](https://efnet-math.org/wiki/images/math/d03ec93f0c0ee0c5891084fdc383ea7f.png) such that
such that  is prime for all sufficiently large primes p.
is prime for all sufficiently large primes p.
Solution
i) is a special case of ii) so we will only solve ii) below.
Let 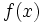 satisfy the condition in ii).
satisfy the condition in ii).
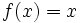 and
and 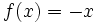 are obviously solutions.
are obviously solutions.
Assume that 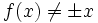 . Then there is a prime
. Then there is a prime 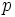 with
with 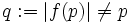 .
Then
.
Then 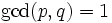 so the sequence
so the sequence  contains infinitely many primes by Dirichlet's theorem (http://en.wikipedia.org/wiki/Dirichlet's_theorem_on_arithmetic_progressions).
contains infinitely many primes by Dirichlet's theorem (http://en.wikipedia.org/wiki/Dirichlet's_theorem_on_arithmetic_progressions).
Let 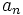 be prime. Because
be prime. Because 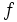 is a polynomial with
integer coefficients,
is a polynomial with
integer coefficients, 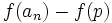 is divisible
by
is divisible
by 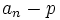 , which in turn is divisible by
, which in turn is divisible by 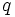 by the
definition of
by the
definition of 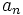 . We also have
. We also have  so
so 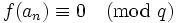 . But
. But 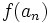 must be prime so that
must be prime so that 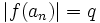 . So
. So 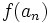 assumes one of the values
assumes one of the values  or
or 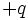 infinitely often which means that it is a constant polynomial.
infinitely often which means that it is a constant polynomial.
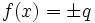 for prime numbers
for prime numbers 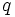 are indeed solutions of ii). There are no other solutions.
are indeed solutions of ii). There are no other solutions.