Problem Of The Day
- Some rules we all encouraged to abide by in the channel
This is efnet-math.org's Problem of the Day section. New problems are added every few days. Problems are archived at the end of the month. This and last month is always kept on this page. To view past problems, browse through the Problem of the Day Archive
July 2012
Monday, July 30, 2012
from breeden
Using only "calculus 1" methods, show that 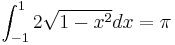 . (trig substitution and polar coordinates is not allowed, but we will allow "improper" integrals). Conclude that
. (trig substitution and polar coordinates is not allowed, but we will allow "improper" integrals). Conclude that 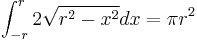 .
.
June 2012
Saturday, June 30, 2012
from hochs
Let L / K be a galois extension of degree 5. If there exists an element 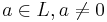 such that a and 5a are conjugates over K, then find all possible characteristics of K. What if 5 is replaced by an arbitrary prime?
such that a and 5a are conjugates over K, then find all possible characteristics of K. What if 5 is replaced by an arbitrary prime?
Wednesday, June 27, 2012
from zeno
Prove that if A is a non-commutative ring with 1, 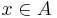 has a right inverse but no left inverse, then x has infinitely many right inverses.
has a right inverse but no left inverse, then x has infinitely many right inverses.
Thursday, June 14, 2012
from hochs
Suppose a ring R is a k-algebra, where k is a field. Suppose A,B,C are left R-modules that are finite dimensional over k, and that there's a split exact sequence 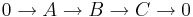 . Prove that every exact sequence
. Prove that every exact sequence 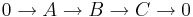 is split.
is split.
Tuesday, June 12, 2012
from hochs
Suppose 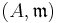 is a complete noetherian local ring, and
is a complete noetherian local ring, and 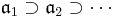 is a decreasing sequence of ideals of A such that
is a decreasing sequence of ideals of A such that 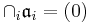 . Then the linear topology defined by
. Then the linear topology defined by 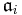 's is finer than the
's is finer than the 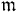 -adic topology on A. That is, for any n > 0, there exists i > 0 such that
-adic topology on A. That is, for any n > 0, there exists i > 0 such that 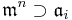 .
.
It's easy to cook up an example where this fails if A is not noetherian. Find a counterexample when A is not complete.
May 2012
Tuesday, May 29, 2012
from Y0UrShAD0
Evaluate 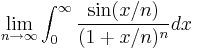 without resorting to the Dominating Convergence theorem.
without resorting to the Dominating Convergence theorem.
Wednesday, May 23, 2012
from lhrrwcc
Let M = (aij) be a 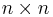 -matrix over a local ring A such that for all i,j: aii is a unit and
-matrix over a local ring A such that for all i,j: aii is a unit and 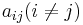 is not a unit. Show that M is a unit in Matn(A).
is not a unit. Show that M is a unit in Matn(A).
Monday, May 21, 2012
from lhrrwcc
Let M be a projective left module over a ring, then there exists a free left module F such that 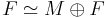 .
.
Solution by hochs
April 2012
Thursday, April 19, 2012
from hochs
For n > 1, let 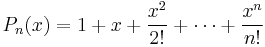 . For n odd, this polynomial has exactly one real root (prove this). Prove that this root is irrational for all odd n > 1.
. For n odd, this polynomial has exactly one real root (prove this). Prove that this root is irrational for all odd n > 1.
Tuesday, April 17, 2012
from joo & Karlo
Suppose that 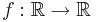 is continuous and satisfies
is continuous and satisfies 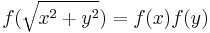 for all
for all 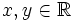 . Then f(x) is identically 0 or
. Then f(x) is identically 0 or 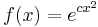 for some
for some 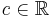 .
.
Sunday, April 15, 2012
from hochs
Suppose 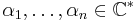 are nonzero complex numbers such that the set
are nonzero complex numbers such that the set 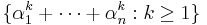 is a finite set. Prove that αi is a root of unity for all i.
is a finite set. Prove that αi is a root of unity for all i.
Tuesday, April 10, 2012
from "spal"
Prove that 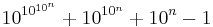 is not a prime for any nonnegative integer n.
is not a prime for any nonnegative integer n.
Friday, April 6, 2012
TGIF
For prime p, show that 2p + 3p is not a perfect power (i.e. not of the form mk for naturals m > 1,k > 1).
Wednesday, April 4, 2012
from breeden
You are given digits 1, 3, 4, 6 and allowed to add, multiply, subtract, divide and use brackets. For example, 4*(6/3+1) gives 12. Can you get 24? No uniting of digits or using powers is allowed, such as in 3*(14-6) or 6*(14+3). You also have to use each digit exactly once, so 4*6 does not work either.
Monday, April 2, 2012
from hochs
Let (K, | | ) be any complete normed field. Prove that any finite dimensional vector space over K has unique norm (up to equivalence of norms), and therefore it is again complete. Remark. This is well-known when 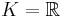 or
or 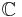 , i.e. when V is a Banach space. The point is that one does not need compactness to prove this slightly more general version.
, i.e. when V is a Banach space. The point is that one does not need compactness to prove this slightly more general version.
Sunday, April 1, 2012
from brett1479
Show that if 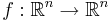 is continuously differentiable and injective, then there exists a non-empty open subset of
is continuously differentiable and injective, then there exists a non-empty open subset of 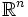 where | det(f'(x)) | > 0.
where | det(f'(x)) | > 0.
March 2012
Saturday, March 31, 2012
from breeden
(a) Show that there exists a (necessarily non-measurable) function 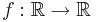 with the property that for any function
with the property that for any function 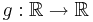 such that
such that 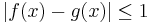 for all
for all 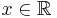 then g is non-measurable.
then g is non-measurable.
(b) Show that there exists a continuous function ![f:[0,1] \to [0,1]](https://efnet-math.org/wiki/images/math/117e263f06305f1177c599895342aa9b.png) and a Lebesgue-measurable set
and a Lebesgue-measurable set ![B \subseteq [0,1]](https://efnet-math.org/wiki/images/math/edd3bb07ca9afdb694c8c200f6415f55.png) such that
such that ![f(B) \subseteq [0,1]](https://efnet-math.org/wiki/images/math/ecef50a2539441b43b647de083e45104.png) is non-measurable. Can you take B to be Borel-measurable? (Hint: One can find such an f that takes a set of null-measure onto [0,1])
is non-measurable. Can you take B to be Borel-measurable? (Hint: One can find such an f that takes a set of null-measure onto [0,1])
Monday, March 26, 2012
Happy Birthday Paul Erdős
How many sequences 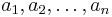 of 1's and − 1's exist such that the number of i with ai = 1 is equal to the number of j with aj = − 1 and all the partial sums
of 1's and − 1's exist such that the number of i with ai = 1 is equal to the number of j with aj = − 1 and all the partial sums 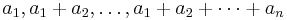 are nonnegative?
are nonnegative?
Saturday, March 24, 2012
from hochs
For a function 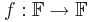 on a finite field
on a finite field 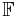 with q elements, one can find a polynomial
with q elements, one can find a polynomial ![F \in \mathbb{F}[x]](https://efnet-math.org/wiki/images/math/a7529d38e5170773604d0546b1dd8ca3.png) such that f(c) = F(c) for all elements
such that f(c) = F(c) for all elements 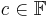 (evaluation at c). If we insist that the degree of this polynomial be less than q, then it is uniquely determined by the function f. We can thus speak of degree of nonzero f as the degree of this associated polynomial.
(evaluation at c). If we insist that the degree of this polynomial be less than q, then it is uniquely determined by the function f. We can thus speak of degree of nonzero f as the degree of this associated polynomial.
Prove that if q is odd, then no permutation (i.e. bijective) map 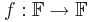 has degree q − 1. What if q is even?
has degree q − 1. What if q is even?
And an optional unsolved problem: What are the possible degrees of permutations? Classify all "permutation" polynomials.
Sunday, March 18, 2012
from hochs
Let ![f \in \mathbb{R}[x]](https://efnet-math.org/wiki/images/math/1e138ad9ffd38e67f2c266f68bdc059e.png) be any nonzero polynomial. Let
be any nonzero polynomial. Let 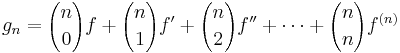 , where f(k) denotes the k-th derivative of f. Prove that there exists a positive integer N such that all roots of gn are real for all
, where f(k) denotes the k-th derivative of f. Prove that there exists a positive integer N such that all roots of gn are real for all 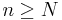 .
.
Saturday, March 17, 2012
from breeden
Let 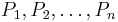 be vertices of a regular n-gon inscibed in a unit circle. Let O denote the center of the circle. Suppose P is a point on the unit circle such that the line segment OP bisects one of the sides PiPi + 1. Show that the product of distances from P to Pi,
be vertices of a regular n-gon inscibed in a unit circle. Let O denote the center of the circle. Suppose P is a point on the unit circle such that the line segment OP bisects one of the sides PiPi + 1. Show that the product of distances from P to Pi, 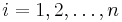 is exactly 2.
is exactly 2.
Saturday, March 17, 2012
from hochs
Let 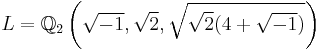 , where
, where 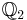 denotes the 2-adic rationals (completion of
denotes the 2-adic rationals (completion of 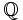 w.r.t. the 2-adic valuation). Show that
w.r.t. the 2-adic valuation). Show that 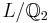 is Galois, find its galois group, and find a uniformizer for L (recall that
is Galois, find its galois group, and find a uniformizer for L (recall that 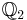 is complete, hence the existence and uniqueness of discrete valuation extending that of
is complete, hence the existence and uniqueness of discrete valuation extending that of 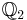 .
.
Thursday, March 15, 2012
from hochs
Denote by Sn the group of permutations of the sequence 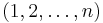 . Suppose that G is a subgroup of Sn, such that for every
. Suppose that G is a subgroup of Sn, such that for every 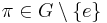 , there exists a unique
, there exists a unique 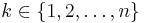 for which π(k) = k. Show that k is the same for all
for which π(k) = k. Show that k is the same for all 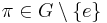 .
.
Wednesday, March 14, 2012
from hochs
Let P(x) be a polynomial with real coefficients. Show that there exists a nonzero polynomial Q(x) with real coefficients such that P(x)Q(x) has terms that are all of a degree divisible by 109
Saturday, March 3, 2012
from hochs
There are two kinds of coins, genuine and counterfeit. A genuine coin weighs X grams and a counterfeit coin weighs X + δ grams, where X is positive integer and δ is non-zero real number strictly between 5 and − 5. You are presented with 13 piles of 4 coins each. All of the coins are genuine, except for one pile, in which all 4 coins are counterfeit. You are given a precise scale (say, a digital scale capable of displaying any real number - wow!). You are to determine three things: X,δ and which pile contains the counterfeit coins. But you’re only allowed to use the scale twice!
February 2012
Wednesday, February 29, 2012
from breeden
Assume that ![f_n: [0,1] \to \mathbb{R}^+](https://efnet-math.org/wiki/images/math/d04f4cb4674c1f441b13a2042c2b7b02.png) are continuous functions where
are continuous functions where 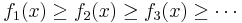 . Let
. Let 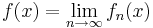 and
and ![M = \sup\{ f(x) : x \in [0,1] \}](https://efnet-math.org/wiki/images/math/fcc1e8be60875524702358c6185f473a.png) . Show that there exists
. Show that there exists ![y \in [0,1]](https://efnet-math.org/wiki/images/math/ab3abad183cd9e117cb5711a60e1bc1d.png) such that f(y) = M.
such that f(y) = M.
Tuesday, February 28, 2012
from breeden
Show that if 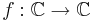 is holomorphic where | f(z) | = 1 whenever | z | = 1 then f(z) = λzn where | λ | = 1 and
is holomorphic where | f(z) | = 1 whenever | z | = 1 then f(z) = λzn where | λ | = 1 and 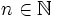 .
.
Friday, February 24, 2012
from hochs
Prove that if ![f,g \in \mathbb{Z}[x]](https://efnet-math.org/wiki/images/math/798a6676d689336aa8a745ce1e7b0b81.png) are coprime polynomials then there are infinitely many positive integers n such that nf + g is irreducible in
are coprime polynomials then there are infinitely many positive integers n such that nf + g is irreducible in ![\mathbb{Z}[x]](https://efnet-math.org/wiki/images/math/1720d8ed9c2582abffc3c0685c1ddb77.png) .
.
Remark: Elementary solution exists. No complex analysis, no L-functions,... are needed.
Thursday, February 23, 2012
from hochs
Show that if p is prime, then 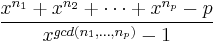 is irreducible over
is irreducible over ![\mathbb{Q}[x]](https://efnet-math.org/wiki/images/math/2e6941566cf570df9666c0d4d6480645.png) . As usual,
. As usual, 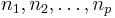 denote positive integers.
denote positive integers.
Solution (http://www.artofproblemsolving.com/Forum/viewtopic.php?f=36&t=395023)
Tuesday, February 21, 2012
from breeden
Does there exist a nowhere continuous function 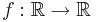 such that f(x + y) = f(x) + f(y) for all
such that f(x + y) = f(x) + f(y) for all 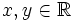 ?
?
Monday, February 20, 2012
from breeden
Show that there exists a constant C such that 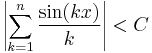 for all
for all 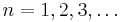 and
and ![x \in [0,2\pi]](https://efnet-math.org/wiki/images/math/6fd9dce3d68bd4a564c71936723fe9f0.png) .
.
Hint: Break the sum into two parts for 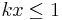 and
and 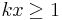 , respectively.
, respectively.
Saturday, February 18, 2012
from breeden
Suppose that 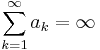 and {bn} is a bounded sequence, where an and bn are real. Show that there exists an increasing sequence of positive integers, nk, such that
and {bn} is a bounded sequence, where an and bn are real. Show that there exists an increasing sequence of positive integers, nk, such that 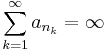 and
and 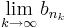 converges.
converges.
Thursday, February 16, 2012
from Zabrien
Let 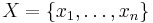 be a set of positive integers with
be a set of positive integers with
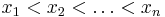 and xn = 2n − 1. Show that the complement of X in the naturals is closed under addition iff for all
and xn = 2n − 1. Show that the complement of X in the naturals is closed under addition iff for all 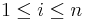 and for all
and for all 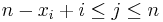 we have
we have 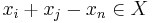 .
.
Wednesday, February 15, 2012
from Zabrien
Consider the vector space ![\mathbb{R}[x_1, \cdots, x_n]](https://efnet-math.org/wiki/images/math/28ff7be45f58b9dd5e94a8f554455d1e.png) of real polynomials in n variables. Let
of real polynomials in n variables. Let
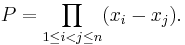
Let X be the subspace spanned by all partial derivatives of P. Show that X has dimension at least n!.
Sunday, February 12, 2012
from hochs
Suppose X is a finite set such that | X | = 2k for some positive integer k. Suppose there's a family F of subsets of X, where each element of F has cardinality k, and such that every subset of X having cardinality k − 1 is uniquely contained in some element of F. Prove that k + 1 is prime.
Solution by hochs
Friday, February 10, 2012
from breeden
Let S be the set of holomorphic functions 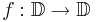 such that f(0) = 0 and
such that f(0) = 0 and 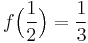 , where
, where 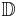 denotes the open unit disc in
denotes the open unit disc in 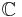 .
.
Determine the value of: 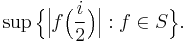
May 2009
Saturday, May 30, 2009
For prime p, prove that 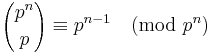 , for all
, for all 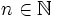
Variation: For odd prime p, prove that 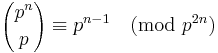 , for all
, for all 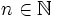
August 2008
Saturday, August 30, 2008
Let f be a holomorphic function on the open unit disc Δ such that | f(z) | < 1 for all 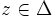 . Suppose that
. Suppose that 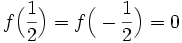 . Show that
. Show that 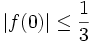 .
.
May 2008
Thursday, May 19, 2008
from Zabrien
Consider a completely filled Sudoku, written as a 9x9 matrix. Show that the determinant of this matrix is divisible by 405.
Solution by int-e
April 2008
Monday, April 7, 2008
from beigebox
Given a set of points 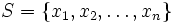 in the plane so that for each two points
in the plane so that for each two points 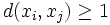 , show that there are at most 3n pairs of points of distance exactly 1.
, show that there are at most 3n pairs of points of distance exactly 1.
from Crito
The sequence 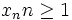 is defined by
is defined by
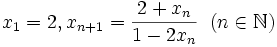 . Prove that
. Prove that
a) for all 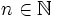 ,
,
b) 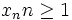 is not periodic.
is not periodic.
March 2008
Friday, March 29, 2008
from Polytope
Solve the following system of equations:
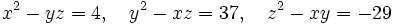
Sunday, March 23, 2008
from dedekind
Does there exist a continuous function f such that f(f(x)) = x2 − 2.
Solution (http://www.artofproblemsolving.com/Forum/viewtopic.php?search_id=778734284&t=103001)
February 2008
January 2008
Friday, 18th of January
Find the number of solutions to y2 = x(x2 + B) over the finite field with p elements where 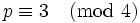 and p does not divide B.
and p does not divide B.
Sunday, 13th of January
posted by Crito
1. A hyper-primitive root is a k-tuple 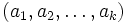 and
and 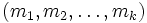 with the following property:
with the following property:
For each 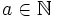 , that (a,m) = 1, has a unique representation in the following form:
, that (a,m) = 1, has a unique representation in the following form:
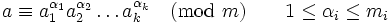
Prove that for each m we have a hyper-primitive root.
2. Let p be prime number and n be non negative integers.
(1) Let m be integer such that 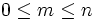 . How many numbers are there among integers 1 through pn + 1 which can be divided by pm not but by pm + 1?
. How many numbers are there among integers 1 through pn + 1 which can be divided by pm not but by pm + 1?
(2) For two integers 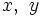 1 through pn + 1, how many pairs of (x, y) such that the product xy can be divided by pn + 1?
1 through pn + 1, how many pairs of (x, y) such that the product xy can be divided by pn + 1?
December 2007
Monday, 17th of December
posted by crito
Find all functions 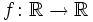 such that
such that
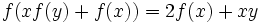 for every reals x,y.
for every reals x,y.
Monday, 10th of December
Let S be a simple random walk on 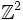 starting at the origin. Show that the probability that S returns to the origin before hitting (1,0) is
starting at the origin. Show that the probability that S returns to the origin before hitting (1,0) is 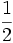 .
.
Tuesday, 4th of December
posted by Crito
Let f(x) = x2 + 2007x + 1. Prove that for every positive integer n, the equation 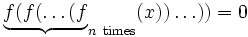 has at least one real solution.
has at least one real solution.
November 2007
Thursday, 29th of November
posted by dioid
Let f(x) = − x2 + 2xsin(x) + cos(2x) prove that f(x) < 0 for 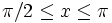
Experienced solvers, please don't spoil it in channel, HS calc level
Wednesday, 28th of November
posted by nerdy2
Classify GL(V) orbits of pairs of nondegenerate symmetric bilinear forms on a vector space V over an algebraically closed field.
Sunday, 18th of November
posted by Crito
Let n be a natural number, such that (n,2(21386 − 1)) = 1. Let  be a reduced residue system for n. Prove that:
be a reduced residue system for n. Prove that:
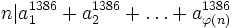
Solution by int-e
Monday, 12th of November
posted by Crito
Let p be a prime number and n be a non-negative integer.
(1) Let m be an integer, 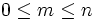 . How many integers k exist,
. How many integers k exist, 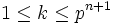 , such that
, such that 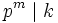 but
but 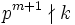 ?
?
(2) How many pairs of integers (x,y) exist such that ![x,y\in\left[1,p^{n+1}\right]](https://efnet-math.org/wiki/images/math/c23e632da30cfc8f71dfb2a050cc1729.png) and
and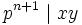 ?
?
Bonus by nerdy2
Given a function 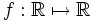 , suppose
, suppose 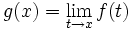 exists everywhere. Show that g is continuous.
exists everywhere. Show that g is continuous.
Sunday, 11th of November
Find the number of integers c such that 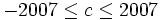 and there exists an integer x such that x2 + c is a multiple of 22007.
and there exists an integer x such that x2 + c is a multiple of 22007.
October 2007
Monday, 22nd of October
Posted by HiLander
Let 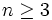 and let F be a collection of subsets of
and let F be a collection of subsets of 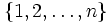 with | F | = 2n − 1 + n + 1. Show that there are
with | F | = 2n − 1 + n + 1. Show that there are 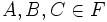 with
with 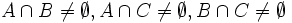 , but
, but 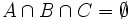 .
.
Monday, 15th of October
Posted by Galois
(A challenge from Fermat to the English mathematicians.)
Find all integer solutions x,y of the equation y2 = x3 − 2.
Saturday, 13th of October
Posted by Crito
Prove that for a set 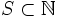 , there exists a sequence
, there exists a sequence 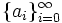 in S such that for each n,
in S such that for each n, 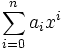 is irreducible in
is irreducible in ![\mathbb Z[x]](https://efnet-math.org/wiki/images/math/3182ba9f80992f4f3bf853027b5dc2a3.png) if and only if
if and only if 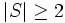 .
.
Extra: Posted by Crito
1. Positive integers x>1 and y satisfy an equation 2x2 − 1 = y15. Prove that 5 divides x.
2. Find integral solutions to the equation (m2 − n2)2 = 16n + 1.
Friday, 12th of October
posted by Crito
a) Let 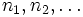 be a sequence of natural number such that
be a sequence of natural number such that 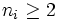 and
and 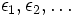 be a sequence such that
be a sequence such that 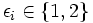 .
Prove that the sequence:
.
Prove that the sequence:
![\sqrt[n_{1}]{\epsilon_{1}+\sqrt[n_{2}]{\epsilon_{2}+\dots+\sqrt[n_{k}]{\epsilon_{k}}}}](https://efnet-math.org/wiki/images/math/fa970f5882a23fa34f391c4f3bd28627.png) is convergent and its limit is in (1,2].
is convergent and its limit is in (1,2].
Define ![\sqrt[n_{1}]{\epsilon_{1}+\sqrt[n_{2}]{\epsilon_{2}+\dots}}](https://efnet-math.org/wiki/images/math/ad2d97a549d92db8e59abab08e23aa4b.png) to be this limit.
to be this limit.
b) Prove that for each ![x\in(1,2]](https://efnet-math.org/wiki/images/math/102086e30114e023dedc4c3654ee996e.png) there exist sequences
there exist sequences 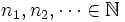 and
and 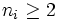 and
and 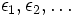 , such that
, such that 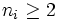 and
and 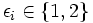 , and
, and ![x=\sqrt[n_{1}]{\epsilon_{1}+\sqrt[n_{2}]{\epsilon_{2}+\dots}}](https://efnet-math.org/wiki/images/math/814d81e01ced68ca6a32cdd83ed24e7e.png)
Friday, 5th of October
posted by Crito
Let n be a natural number, and n = 22007k + 1, such that k is an odd number. Prove that 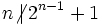
Wednesday, 3rd of October
posted by Crito
Sequence {an} is defined by 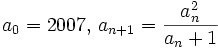 for
for 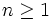 . Prove that
. Prove that 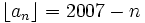 for
for 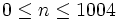 , where
, where 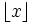 denotes the largest integer no larger than x.
denotes the largest integer no larger than x.
Solution by int-e.
September 2007
Friday, 28th of September
posted by Crito
Find all positive integers k with the following property: There exists an integer a so that (a + k)3 − a3 is a multiple of 2007.
Thursday, 27th of September
posted by Crito
Let a,b,c,d be real numbers which satisfy 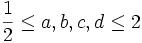 and abcd=1. Find the maximum value of
and abcd=1. Find the maximum value of
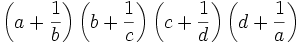 .
.
Wednesday, 26th of September
posted by Crito
Let a,b,c,d be positive real numbers with a+b+c+d = 4.
Prove that 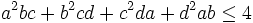 .
.
Tuesday, 25th of Septemeber
posted by Crito
Determine all pairs (x,y) of positive integers satisfying the equation x! + y! = xy.
Saturday, 22nd of September
posted by Crito
Prove that for two non-zero polynomials f(x,y),g(x,y) with real coefficients the system:
f(x,y)=0
g(x,y)=0
has finitely many solutions in 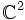 if and only if f(x,y) and g(x,y) are coprime.
if and only if f(x,y) and g(x,y) are coprime.
Thursday, 20th of Setember
posted by Crito
Does there exist a sequence 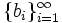 of positive real numbers such that for each natural m:
of positive real numbers such that for each natural m: 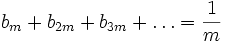
Solution by int-e.
Wednesday, 19th of September
posted by Crito
Given an integer m, define the sequence 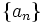 as follows:
as follows:
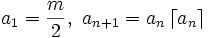 if
if 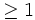 Find all values of m for which a2007 is the first integer appearing in the sequence.
Find all values of m for which a2007 is the first integer appearing in the sequence.
Friday, 14th of September
from \\Steve
If H,G are groups, let 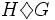 denote that H < G such that for every automorphism
denote that H < G such that for every automorphism 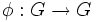 and
and 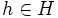 ,
, 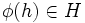 . Let
. Let 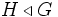 denote that H is a normal subgroup of G.
If
denote that H is a normal subgroup of G.
If 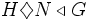 , show that
, show that 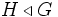 .
.
Tuesday, 11th of September
posted by Crito
Let a and b be positive integers. Show that if 4ab − 1 divides (4a2 − 1)2, then a = b.
Solution by int-e.
Saturday, 1st of September
posted by Crito
Let p > 5 be a prime number.
For any integer x, define 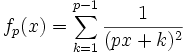
Prove that for any pair of positive integers x, y, the numerator of fp(x) − fp(y), when written as a fraction in lowest terms, is divisible by p^3.
August 2007
Wednesday, 29th of August
posted by Crito
Let 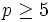 be a prime.
be a prime.
(a) Show that exists a prime 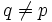 such that q | (p − 1)p + 1
such that q | (p − 1)p + 1
(b) Factoring in prime numbers 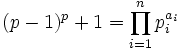 show that:
show that:
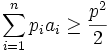
Saturday, 11th of August
Prove that the set of strict local maximum points of a real function is countable.
Solution (http://encyclomaniacs.sound-club.org/~fs/math/POTD-2007-08-11.pdf) by flamingspinach
July 2007
Thursday, 26th of July
edited by landen, not in Easy Series
Find the following limit in terms of 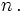
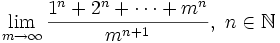
For a gold star try it for 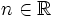 with
with 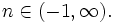
Solution from landen
Saturday, 21st of July
Problem 6 from landen's Easy Series
Might be a little harder than usual.
What is the largest positive integer 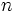 such that
such that 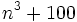 is divisible by
is divisible by 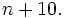
Solution by int-e.
Tuesday, 3rd of July
Problem 5 from landen's Easy Series
from John of Palermo about 1224 CE
Three men own a share in a heap of coins; the first owns 1/2, the second 1/3, and the third 1/6. The money is divided by having each man take an amount arbitrarily. The first man returns 1/2 of the coins he has taken, the second 1/3, and the third 1/6. The money thus returned is divided into three equal shares, which are given to each man, and it turns out that now everyone has his proper part. How much money was there, and how much money did each obtain the first time?
Problem 6 Easy Series
Six positive integers form a strictly increasing series. Each number except the first is a multiple of the preceding number. Their sum is 79. Find out all you can about the numbers.
June 2007
Friday, 29th of June
2 more from landen's Easy Series
Show that the rational number
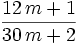
is in lowest terms for any positive integer m.
A cube has all sides labeled with a positive integer. Then at each corner of the cube the corner is labeled with the product of the numbers on the three sides that come together at the corner. The sum of the numbers from all 8 corners is 1001. What is the sum of the 6 numbers on the sides?
Solutions by int-e.
Thursday, 28th of June
NEW!! landen's Easy Series. Formal training not required.
Find all positive integers 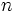 such that
such that 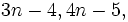 and
and 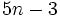 are all prime numbers.
are all prime numbers.
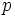 and
and 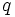 are prime numbers.
are prime numbers. 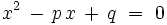 has distinct rational roots. Find all
has distinct rational roots. Find all 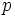 and
and 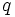 which work.
which work.
Solutions by int-e.
Monday, 25th of June
Posted by Crito
Let 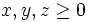 be real numbers. Prove that:
be real numbers. Prove that: 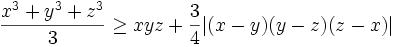 .
.
Find the maximal real constant α that can replace 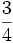 such that the inequality is still true for any non-negative x,y,z.
such that the inequality is still true for any non-negative x,y,z.
Sunday, 24th of June
Posted by Crito
If F is a finite set of at least three positive integers each dividing the sum 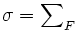 , where gcd(F) = 1, show that the product
, where gcd(F) = 1, show that the product 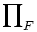 divides
σ | F | − 2.
divides
σ | F | − 2.
Friday, 22nd of June
Posted by Crito
Does there exist a a sequence 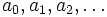 in
in 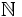 , such that for each
, such that for each 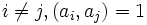 , and for each n, the polynomial
, and for each n, the polynomial 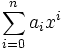 is irreducible in
is irreducible in ![\mathbb Z[x]](https://efnet-math.org/wiki/images/math/3182ba9f80992f4f3bf853027b5dc2a3.png) ?
?
Solution by int-e.
Tuesday, 14th of June
Posted by Crito
Let k be a given natural number. Prove that for any positive numbers x; y; z with the sum 1 the following inequality holds:
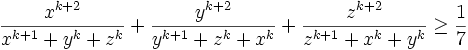 .
When does equality occur?
.
When does equality occur?
Sunday, 10th of June
Posted by Crito
Determine all pairs of natural numbers (x; n) that satisfy the equation x3 + 2x + 1 = 2n.
Tuesday, 5th of June
Posted by Crito
Let 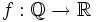 be a function such that
be a function such that 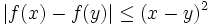 for all
for all 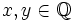 . Prove that f is constant.
. Prove that f is constant.
Sunday, 3rd of June
Posted by Crito
i) Find all infinite arithmetic progressions of positive integers 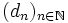 such that dp is prime for all sufficiently large primes p.
such that dp is prime for all sufficiently large primes p.
ii) Find all polynomials ![f(X) \in \mathbb{Z}[X]](https://efnet-math.org/wiki/images/math/d03ec93f0c0ee0c5891084fdc383ea7f.png) such that
such that 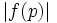 is prime for all sufficiently large primes p.
is prime for all sufficiently large primes p.
Solution by int-e.
Saturday, 2nd of June
Posted by Crito
Find all polynomials of degree 3, such that for each 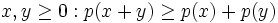
Solution by int-e.
May 2007
Wednesday, 30th of May
Posted by Crito
Let a,b,c,d be positive reals such that a + b + c + d = 1.
Prove that: 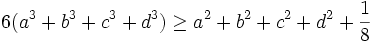 .
.
Solution by int-e
Tuesday, 29th of May
Posted by Crito
Does there exist two unfair 6-sided dice labeled with numbers
1..6 each such that probability of their sum being j is a number in 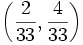 for each
for each 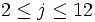 ?
?
Solution by int-e
Bonus posted by Crito
Prove that the function 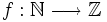 defined by f(n) = n2007 − n!, is injective.
defined by f(n) = n2007 − n!, is injective.
Friday, 25th of May
Posted by Crito
Natural numbers a, b and c are pairwise distinct and satisfy a | b + c + bc,b | c + a + ca,c | a + b + ab.
Prove that at least one of the numbers a, b, c is not prime.
Solution by int-e.
Tuesday, 22nd of May
Suggested by feydrauth
Prove or disprove:
For any positive integer 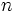 there is a positive integer
there is a positive integer 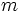 such that
such that 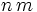 has only 0's and 7's as decimal digits.
has only 0's and 7's as decimal digits.
Solution by int-e.
Friday, 18th of May
poted by Crito
Find all real α,β such that the following limit exists and is finite:
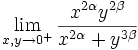
Friday, 11th of May
from Magnuss
Determine whether there exists a function 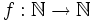 such that
such that 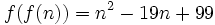 for all positive integers
for all positive integers