A FAQ is how to show that ![]() converges.
converges.
There are several proofs for students with different backgrounds and interests. Each one has its own advantages.
There is a powerful theorem in real analysis which will prove convergence of this and many other series. It is surprisingly easy to prove if you take the right path. The general theorem is called Dirichlet's Test. This link proves it under the name Abel's Test. Abel's Test usually refers to a weaker theorem. Using the Dirichlet Test it is sufficient to show that:
![]() is bounded and that the sequence {1/n} converges monotonically to 0.
is bounded and that the sequence {1/n} converges monotonically to 0.
A way to prove boundedness without complex analysis is to use the trig identity
![]()
This gives a telescoping sum for
![]()
This means the partial sums are between between ![]() and
and ![]()
Showing that 1/n converges monotonically to zero as n → ∞ is left as an exercise for the reader.
Start with a numerical investigation just to see what happens. The sum of M = 105 terms of the series ![]() gives 0.0420148, and 105 + 1 terms gives .0420091. The numerical news is not encouraging. Even after 105 terms the 5th decimal place is barely trustworthy. This series converges very slowly at best. There is a method of converting this series to one that converges faster. This idea proves convergence and gives a better value for the sum.
gives 0.0420148, and 105 + 1 terms gives .0420091. The numerical news is not encouraging. Even after 105 terms the 5th decimal place is barely trustworthy. This series converges very slowly at best. There is a method of converting this series to one that converges faster. This idea proves convergence and gives a better value for the sum.
![]() leads to:
leads to:
![]()
![]()
![]() .
.
So this new series converges absolutely:
![]() .
.
This series converges fast enough to enable feasible computation of the limit.
| Terms | Original | New |
|---|---|---|
| 100 | 0.0416039 | 0.0419236 |
| 1000 | 0.0430569 | 0.0420199 |
| 10000 | 0.0419439 | 0.0420195 |
By using calculus we can get a more convenient, compact answer that is easy to evaluate to many decimal places using software for the common functions. Reconsider ![]() .
.
In order to use the power of calculus on this, we consider a function of x rather than just integers. We also are going to sum sin(nx) instead of cos(nx) in order to use a trick later. A telescoping trig identity for sin(nx) is:
![]()
Summing both sides of that from n = 1 to M we get for the partial sum via telescoping terms:
![]()
Now, the trick is to use integration to change sin(nx) into -cos(nx)/n. So we integrate both sides from 1 to π, which happens to be convenient:
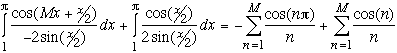
Now we have to evaluate the terms of this partial sum and take the lim M → ∞. For the first sum on the right:
![]() . Notice cos(nπ) = (-1)n and use the Taylor series
. Notice cos(nπ) = (-1)n and use the Taylor series ![]() .
.
For the second integral on the left, elementary calculus gives:
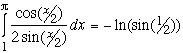
Consider the messier first integral:
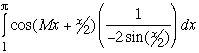
This integral has some interesting features. It could be attacked using the Riemann-Lebesgue Lemma. But in the spirit of making this accessible to Calc I students there is an long but elementary proof in this special case. Call ![]() . g(x) is bounded and so is g'(x) for x between 1 and π. So we integrate by parts:
. g(x) is bounded and so is g'(x) for x between 1 and π. So we integrate by parts:
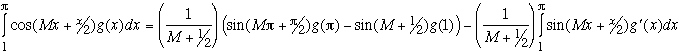
![]() , by elementary inequalities.
, by elementary inequalities.
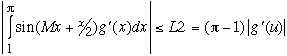 , where u is a point between 1 and π at which |g'(u)| has its maximum value. You can find such a point with elementary calculus.
, where u is a point between 1 and π at which |g'(u)| has its maximum value. You can find such a point with elementary calculus.
If on a first reading you get lost, notice that L1 and L2 are explicit numbers, not variables or functions or anything.
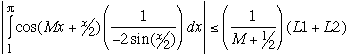 .
.
When M → ∞ the limit of this integral is 0. This is actually intuitive if you notice that cos(Mx + x/2) "chops up" the continuous and bounded integrand into finer and finer adjacent pieces of opposite sign.
Putting all the parts together we have the very compact answer:
![]() = 0.04201950582536896172579838403,
= 0.04201950582536896172579838403,
approximately, using software for ln(x) and sin(x). It would be very hard to get this much accuracy by directly summing cos(n)/n because it converges very slowly.
Created on November 29, 2002